Der Satz des Thales sagt aus, dass alle Winkel auf einem Halbkreisbogen rechte Winkel sein müssen. Diese Aussage wird dem griechischem Phillosophen Thales von Milet zugestanden, der den Satz zwar tatsächlich mathematisch bewiesen hat, aber bekannt war der Satz schon vor seiner Zeit im alten Babylon. Nur keine Angst, es wird auf jeden Aspekt des Satz des Thales eingegangen, dass am Ende jeder Besucher das Prinzip und die Anwendung verstanden hat. Weiter unten findet man eine Menge Übungsaufgaben und Erklärungen.
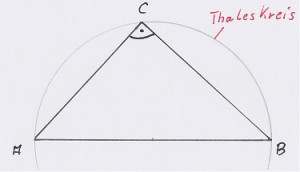
Der Satz des Thales sagt nichts anderes, dass wenn auf dem Thaleskreis ( der Thaleskreis ist der Halbkreis um die längste Seite des Dreiecks ) ein Dreickeck einzeichnet, wird dieses immer rechtwinklig sein. Auf diesem kleinen Bild hier ist die Hypothenuse die Strecke zwischen den Punkten A und B. Der Thaleskreis hat den Durchmesser eben dieser Strecke. Punkt C kann somit frei auf dem Thaleskreis gewählt werden und bildet immer einen rechten Winkel.
Definition Satz des Thales
Die korrekte Definition für den Satz des Thales lautet:
Konstruiert man ein Dreieck aus den beiden Endpunkten des Durchmessers eines Halbkreises (Thaleskreis) und einem weiteren Punkt dieses Halbkreises, so erhält man immer ein rechtwinkliges Dreieck.
Weitere Definitionen ebenfalls richtige Definitionen lauten:
- Alle Winkel am Halbkreisbogen sind rechte Winkel.
- Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C immer einen rechten Winkel.
- Hat das Dreieck ABC bei C einen rechten Winkel, so liegt C auf einem Kreis mit dem Durchmesser AB.
- Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse
Auf den folgenden Seiten findet man noch mehr Erklärungen zum Satz des Thales, sowie der dazugehörige Beweis und vor allem auch Übungsaufgaben.
Anleitung und Erklärung zum Satz des Thales
Anleitung und Erklärung Thaleskreis
Thales von Milet – Leben und Zitate
Praktischer Nutzen Satz des Thales
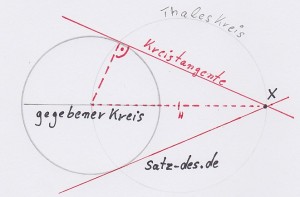
Eine der wichtigsten praktischen Anwendung ist die konstruktion von Kreistangenten von einem außerhalb des Kreises gelegenen Punkt. Eine Tangente ist eine Gerade, die eine geometrische Figur in genau einem Punkt berührt. In diesem Beispiel ist der linke Kreis gegeben, sowie Punkt X. Zeichnet man nun einen Thaleskreis mit dem Durchmesser vom ersten Kreismittelpunkt bis zum Punkt X, schneidet dieser den gegebenen Kreis im Punkt der Kreistangente zu X. Man beachte, dass durch Spiegelung immer zwei Schnittpunkte entstehen und beide Schnittpunkte des Kreises darstellen.
Wer den Satz des Thales nicht verstanden hat, sollte unbedingt unseren Artikel mit der einfachen und verständlichen Erklärung zum Satz des Thales lesen. Den Besuchern, welche noch nicht sicher in der Anwendung sind, seien unsere Übungsaufgaben ans Herz gelegt. Und wer noch mehr über den Phillosophen Thales von Milet und der Hintergrundgeschichte vom Thalessatz lesen möchte, darf gerne in unsere kleine Vita von ihm lesen.