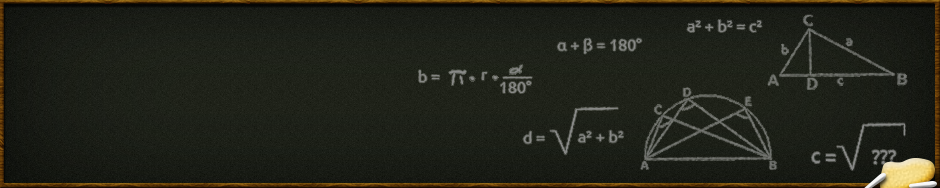In diesem Artikel werden einige Anwendungsbeispiele aufgeführt: Wie man ein rechtwinkliges Dreieck nach dem Satz des Thales konstruieren kann –  nach verschiedenen Vorgaben und leicht verständlich erklärt.

Satz des Thales – Übungen und Anwendungsbeispiele

Konstruktion von rechtwinkligen Dreiecken

1) Rechtwinkliges Dreieck mit rechtem Winkel im Punkt C

Satz des Thales - Rechter Winkel in C

Maße: c = 8 cm, b = 4 cm

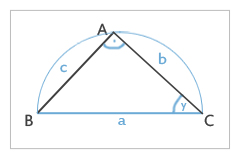
Gegenüber des rechten Winkels im Punkt C liegt die Seite c, welche auch die Strecke AB darstellt. Diese wiederum ist auch der Durchmesser des Thaleskreises. Diese sollte als erstes gezeichnet werden, da Du hierfür den genauen Wert bereits hast.

a ist die Seite, die zuletzt eingezeichnet wird; von b kennen wir die Maße, müssen jedoch erst den Winkel herausfinden. Das können wir ganz einfach tun, ohne ihn ausrechnen zu müssen.

Zuerst einmal müssen wir den Mittelpunkt M herausfinden. Wir wissen, der Durchmesser ist c = AB = 8cm. Wir können also einfach c / 2 rechnen und haben den Radius, ergo die Länge der Strecke, die von AB abgemessen werden muss, um zum Mittelpunkt M zu kommen.

Den Radius r brauchen wir auch direkt wieder, weil wir nun im Punkt M ansetzen und den Thaleskreis über AB zeichnen. Wir wissen, dass der Punkt C nun, um einen Winkel von 90° zu haben, auf diesem Halbkreis sitzen muss.

Kommen wir zu b: b hat die Länge 4cm. Vom Punkt A aus ist also der Punkt C genau 4cm entfernt. Wir zeichnen also nun, angesetzt an Punkt A, einen Kreis mit radius r = 4cm und sehen, dass unsere beiden Kreise sich nun an einem Punkt schneiden. Dieser Punkt ist der einzige Punkt, an dem Punkt C sowohl auf dem Thales Kreis liegen, als auch eine Länge von 4cm haben kann – hier haben wir also Punkt C. Nun muss nur noch die Strecke b = AC von A bis zu unserem Punkt C eingetragen werden und C mit B verbunden werden. Und fertig ist das Dreieck mit rechtem Winkel in Punkt C.

Umgekehrt, wenn Strecke b vorgegeben ist, wird das einfach genauso gemacht.

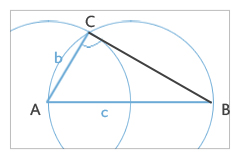
2) Jetzt soll das Dreieck mit rechtem Winkel in B rechtwinklig und gleichschenklig sein

Rechtwinklig und Gleichschenklig

Maße: b = 8 cm

Da auch hier Strecke b gegenüber dem rechten Winkel in Punkt B liegt, beginnen wir auch hier wieder mit b.

Da beide Schenkel gleich lang sein sollen, muss hier die Mittelsenkrechte von b den Punkt B schneiden.

Du brauchst also zuerst den Mittelpunkt M.

Wieder zeichnest Du anschließend den Thaleskreis über CA ein und, wie wir ja bereits bemerkt haben, beide Schenkel genau gleich lang sein sollen, müssen wor die Senkrechte natürlich in die Mitte von CA setzen. Wir setzen dazu im Punkt M an und zeichnen die Senkrechte, bis sie den Kreis schneidet. Das ist unser Punkt B.

Nun müssen nur noch die Punkte CB und BA verbunden werden – da Punkt B auf dem Thales Kreis liegt, ist er bereits rechtwinklig.

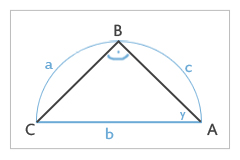
3) Und wenn nun eine bestimmte Höhe h vorgegeben ist?

Vorgegebene Höhe

Maße: Höhe = 5cm

Rechter Winkel in C.

Hier hast Du keine der Strecken tatsächlich vorgegeben. Der Weg dahin ist aber ganz einfach:

 

Du hast hier lediglich die Höhe h. Da Punkt C ja ein rechter Winkel sein muss, weißt Du, er muss auf dem Halbkreis liegen und die Höhe, also Senkrechte h muss in der Strecke c ansetzen, da die Höhe sonst nicht 5cm wären.

Daraus schließen wir, die höhe h ist automatisch gleich dem Radius r des Thaleskreises.

Und wenn r = 5cm ist, ist der Durchmesser = Strecke AB = (r*2), also 10cm.

Nun können wir Strecke c einzeichnen, unseren Mittelpunkt M einzeichnen und die Senkrechte h hinzufügen. Wenn wir alles korrekt machen wollen, zeichnen wir nun noch den Thaleskreis ein und verbinden CA und CB. Den Thaleskreis einzuzeichnen, ist hier kein zwingender Schritt, da h = r ist und C somit auf dem Kreis liegt.

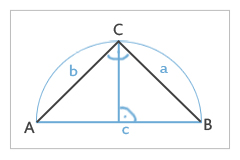
4) Hier ein rechtwinkliges Dreieck, in welchem der Winkel y vorgegeben ist.

Rechter Winkel in A und y ist vorgegeben

Der rechte Winkel soll hier im Punkt A liegen.

Maße: a = 8cm, y = 60°

a ist die Strecke BC gegenüber dem rechten Winkel in A, kann also wieder als Grundstrecke genommen werden.

Hier ist es noch einfacher: Die Strecke BC wird also gezeichnet, der Mittelpunkt M ermittelt und wieder wird der Thaleskreis mit Radius r = BC / 2 eingezeichnet.

Nun wird im Punkt C der Winkel y = 60° ausgemessen und in diesem Winkel eine Strecke CA bis zum Halbkreis gezeichnet. Ist das geschehen, siehst Du Punkt A auf dem Thales Kreis und musst diesen nur noch mit Punkt B verbinden.

Zum Abschluss noch ein paar Tips

• Soll ein Quadrat oder Rechteck nach dem Satz des Thales gezeichnet oder berechnet werden, stellt Euch das Rechteck als zwei zusammengeklebte Dreiecke vor: Die Diagonale stellt die dem rechten Winkel gegenüberliegende Strecke dar. Somit habt Ihr zwei gleich große Dreiecke und wieder die Ausgangssituation wie bei einem Dreieck.
• Wenn Ihr vom Punkt M ausgehend keinen Halbkreis, sondern einen ganzen Kreis einzeichnet und z.B. in Beispiel 1) nicht den Punkt oberhalb des Durchmessers, sondern unterhalb nehmt, erhaltet Ihr eine Spiegelung von gleicher Größe.
• Wenn Ihr, bleiben wir beim Beispiel 1), auf dem oberen Halbkreis alles macht wie in Beispiel 1, auf dem unteren Halbkreis aber Strecke a statt Strecke b die Länge von 4 cm zuweist, erhaltet Ihr ein Rechteck mit 4 rechten Winkeln. Beide Diagonalen haben in diesem Fall dieselbe Länge.