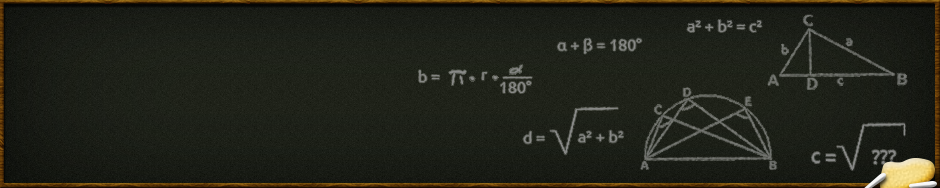 Der Satz des Pythagoras sagt aus, dass die Summe aller Quadrate über den Katheten eines rechtwinkligen Dreiecks gleich dem Quadrat der Hypotenuse ist. Diese Aussage wird dem griechischem Philosophen und Gelehrtem Pythagoras von Samos zugeschrieben. Es handelt sich hierbei um eine recht schillernde und auch heute noch umstrittene Person der Antike. In diesem Artikel wird auf jeden Aspekt des Satz des Pythagoras eingegangen, so dass am Ende jeder Besucher das Prinzip und die Anwendung verstanden hat. Weiter unten findet man eine Menge Übungsaufgaben und Erklärungen, sowie den mathematischen Beweis.
Der Satz des Pythagoras sagt aus, dass die Summe aller Quadrate über den Katheten eines rechtwinkligen Dreiecks gleich dem Quadrat der Hypotenuse ist. Diese Aussage wird dem griechischem Philosophen und Gelehrtem Pythagoras von Samos zugeschrieben. Es handelt sich hierbei um eine recht schillernde und auch heute noch umstrittene Person der Antike. In diesem Artikel wird auf jeden Aspekt des Satz des Pythagoras eingegangen, so dass am Ende jeder Besucher das Prinzip und die Anwendung verstanden hat. Weiter unten findet man eine Menge Übungsaufgaben und Erklärungen, sowie den mathematischen Beweis.
In eine mathematische Formel gepackt lautet der Satz des Pythagoras: a²+b²=c² Hieraus ergeben sich vielfältige Anwendungen zur Berechnung eines rechtwinkligen Dreiecks, sowie teilweise die Feststellung, ob es sich überhaupt um ein rechtwinkliges Dreieck handelt.
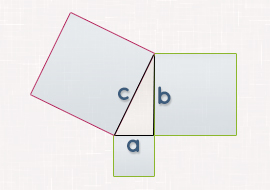
 Definition Satz des Pythagoras
Definition Satz des Pythagoras
Die korrekte Definition für den Satz des Pythagoras lautet:
In allen rechtwinkligen Dreiecken ist die Summe der Fläche der Kathetenquadrate gleich dem Flächeninhalt des Hypothenusenquadrates.
Weitere Definitionen ebenfalls richtige Definitionen lauten:
- In einem rechtwinkligen Dreieck gilt, 1. Kathete zum Quadrat plus 2. Kathete zum Quadrat gleich dem Quadrat der Hypotenuse.
- Ist das Quadrat aus der Summe der Katheten in einem Dreieck gleich dem Quadrat der Fläche über der Hypothenuse, so handelt es sich um ein rechtwinkliges Dreieck.
Auf den folgenden Seiten findet man noch mehr Erklärungen zum Satz des Pythagoras, sowie der dazugehörige Beweis und vor allem auch Übungsaufgaben.
Anleitung und Erklärung zum Satz des Pythagoras
Praktischer Nutzen Satz des Pythagoras
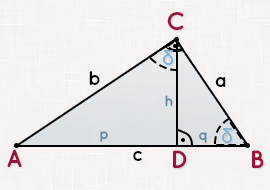 Mittels des Pythagoreische Tripel lassen sich rechtwinklige Dreiecke mittels einer Schnur legen. Durch die Umkehrung des Pythagorassatzes lässt sich bestimmen ob ein Dreieck rechtwinklig ist. Mit dem eigentlichen Satz des Pythagoras kann man bei zwei bekannten Seiten eines rechtwinkligen Dreiecks die jeweils fehlende Seite mathematisch exakt berechnen. Der Satz des Pythagoras dient also vor allem zur Berechnung von Strecken im rechtwinkligen Dreieck. Auch heute noch wird er zum Beispiel zum Vermessen von Flächen verwendet.
Mittels des Pythagoreische Tripel lassen sich rechtwinklige Dreiecke mittels einer Schnur legen. Durch die Umkehrung des Pythagorassatzes lässt sich bestimmen ob ein Dreieck rechtwinklig ist. Mit dem eigentlichen Satz des Pythagoras kann man bei zwei bekannten Seiten eines rechtwinkligen Dreiecks die jeweils fehlende Seite mathematisch exakt berechnen. Der Satz des Pythagoras dient also vor allem zur Berechnung von Strecken im rechtwinkligen Dreieck. Auch heute noch wird er zum Beispiel zum Vermessen von Flächen verwendet.
Wer den Satz des Pythagoras nicht verstanden hat, sollte unbedingt unseren Artikel mit der einfachen und verständlichen Erklärung zum Satz des Pythagoras lesen. Den Besuchern, welche noch nicht sicher in der Anwendung sind, seien unsere Übungsaufgaben ans Herz gelegt. Und wer noch mehr über den Philosophen Pythagoras von Samos und der Hintergrundgeschichte vom Pythagorassatz lesen möchte, darf gerne in unsere kleine Vita von ihm schauen.