Hier die Lösung zur 5. Üburngsaufgabe im Bereich Satz des Thales. Die Aufgabe lautete: “Gegeben sei ein Dreieck mit alpha = 40°, beta = 50°. Die Strecke AB hat eine Länge von 5 cm. Zeichne das Dreieck. Zeige grafisch, ob das Dreieck auf dem Thaleskreis liegt oder nicht.”

Lösung Übungsaufgabe 5 – Satz des Thales

Lösungsdreieck Satz des Thales

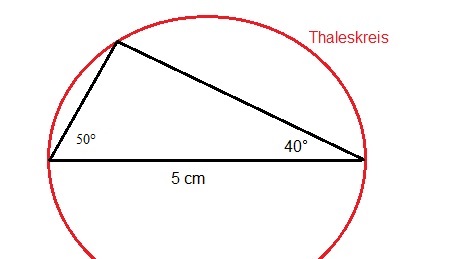
Zeichnet man das Dreieck, so sieht man, dass es auf dem Thaleskreis liegt. Man kann dies auch rechnerisch beweisen, denn die beiden Winkel zusammen ergeben 90° und somit bleibt für die Winkelsumme von 180° im Dreick noch 90° übrig. Somit handelt es sich um ein rechtwinkliges Dreieck und muss folglich auf dem Thaleskreis liegen.

Den Thaleskreis kann man hier einzeichnen, indem man einen Kreis mit dem Durchmesser AB=5 cm um den Mittelpunkt dieser Strecke zeichnet. Mit dem Geodreieck sauber abgemessene Winkel ergeben ein Dreick, welches dem Satz des Thales entspricht.

Zurück zu den Aufgaben zum Satz des Thales geht es über diesen Link hier.