Diese Seite behandelt den Kathetensatz und den Höhensatz des Euklid. Diese beiden Sätze werden benutzt um weitere Berechnungen im rechtwinkligen Dreieck anstellen zu können. Unter anderem werden der Kathetensatz und Höhensatz einzeln dargestellt, einfach erklärt und bewiesen. Wer sich mit den Berechnungen im rechtwinkligen Dreieck noch nicht sicher fühlt, sollte zunächst die Beiträge zum Satz des Thales und den Satz des Pythagoras durcharbeiten.
Der Höhensatz und Kathetensatz des Euklid
Der Höhensatz und Kathetensatz des Euklid
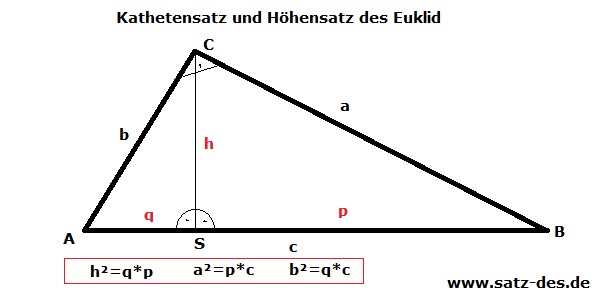
Die Sätze des Euklid beziehen sich die Mathematik im rechtwinkligen Dreieck, wenn man zum Beispiel mit der Höhe des Dreiecks rechnet. Zudem schneidet die Höhe (h) die Hypotenuse eines rechtwinkligen Dreiecks und lässt so die Teilabschnitte q und p entstehen.
Der Höhensatz des Euklid: h²=q*p
Der Kathetensatz des Euklid: a²=p*c und b²=q*c
Auf den folgenden Seiten findet man noch mehr Erklärungen zum Höhen- und Kathetensatz des Euklid, sowie der dazugehörige Beweis und vor allem auch Übungsaufgaben.
Anleitung und Erklärung Kathetensatz und Höhensatz des Euklid
Beweis Höhensatz und Kathetensatz des Euklid
Aufgaben Höhensatz und Kathetensatz des Euklid
Euklid von Alexandria – Wissen
Definition Höhensatz und Kathetensatz
Die korrekte Definition für den Höhensatz lautet
Das Quadrat der Höhe in einem rechtwinkligen Dreieck, entspricht dem Produkt der Hypotenusenabschnitte.
Dementsprechend lauten die Definitionen für beide Kathetensätze:
Das Quadrat der Kathete im rechtwinkligen Dreieck entspricht dem Produkt der Hypotenuse und des darunterliegenden Hypotenusenabschnitts bis zum Lotfußpunkt.