Eine Erklärung zum Satz des Pythagoras und den Bezeichnungen der einzelnen Bestandteile eines rechtwinkligen Dreieckes.
Satz des Pythagoras – Erklärungen
1. Was heißt denn nun a²+b²=c² und was sind a, b und c?
Das rechtwinklige Dreieck mit allen Bezeichnungen
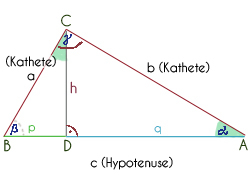
An der Zeichnung können wir nun alle Symbole sehen und erkennen:
- Punkt C liegt gegenüber der Strecke c, wie Punkt B gegenüber Strecke b und Punkt A gegenüber Strecke a liegt.
- Die Höhe h wird im Punkt C angesetzt und steht senkrecht zu Strecke c.
- Auch die Winkelplatzierung kann man sich ganz gut mit Hilfe des Gehörs merken.
Winkel α (Alpha) liegt bei Punkt A, Winkel β (Beta) liegt bei Punkt B und der rechte Winkel γ (Gamma) liegt in Punkt C.
Die beiden Seiten, die direkt am rechten Winkel liegen, a und b, heißen immer Katheten.
Die Strecke, die dem rechten Winkel gegenüber liegt, ganz gleich, ob dieser an der oberen Seite, links, rechts oder unten liegt, heißt Hypotenuse.
Was nun Pythagoras mit a²+b²=c² ausdrücken wollte, ist, dass das das Quadrat aus der Hypotenuse immer den selben Wert hat wie die Summe der Quadrate der beiden Katheten. Man könnte also auch sagen 1.Kathethe²+2.Kathete²=Quadrat der Hypotenuse.
Testlauf
Neues Dreieck durch die Teilung mit Höhe h
Mit etwas logischem Nachdenken und dem eben gelesenen können wir also schlussfolgern:
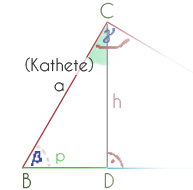
Teilt man nun durch die senkrechte Höhe h dieses Rechtwinklige Dreieck in zwei Hälften, erhält man im Punkt D, in dem ja der neue rechte Winkel liegt, für dieses neue, kleinere Dreieck nun den Punkt C. Aus dem alten Punkt C wird A und da der Winkel β sich nicht verändert hat, der rechte Winkel immer 90° beträgt und die Summe aller Winkel in einem Dreieck stets 180° ergibt, muss also nun der neue Winkel α den selben Wert ergeben, wie der Winkel α im ursprünglichen Dreieck.
2. Wo kann der Satz des Pythagoras angewendet werden?
Ganz simpel: Nur bei Dreiecken mit rechtem Winkel und in der Verlängerung ebenso in rechtwinkligen Vierecken findet er Verwendung. Warum in rechtwinkligen Vierecken? Weil man, teilt man diese diagonal in zwei Hälften auf, zwei rechtwinklige Dreiecke mit denselben Maßen erhält, welche man nur mal 2 nehmen muss, um auf die Gesamtmaße zu kommen, über welche man schließlich auch die Fläche errechnen kann.
Hauptsächlich wird der Satz des Pythagoras dazu verwendet, aus zwei bekannten Strecken eine unbekannte zu berechnen oder aber durch drei bekannte Streckenlängen zu errechnen, ob in einem Dreieck ein rechter Winkel vorkommen kann.
- Die Formeln zum Errechnen der einzelnen Strecken:
a=√(c²-b²)
b=√(c²-a²)
c=√(a²+b²)
Merke: Wird eine der Katheten berechnet, muss unter der Wurzel die jeweils andere Kathete² von der Hypotenuse² subtrahiert werden. Wird jedoch die Hypotenuse errechnet, muss unter der Wurzel 1.Kathete² zu 2. Kathete² addiert werden.
- Um zu berechnen, ob ein Dreieck mit den Seitenlängen, sagen wir a= 3, b = 5 und c = 7 rechtwinklig ist, müsste man folgendermaßen vorgehen:
3²+5² = 9+25 = 34
Da 7² = 49 ergibt und unser Ergebnis aber 34 lautete, ist dieses Dreieck wohl kein rechtwinkliges!
Wer sich weiter über den Satz des Pythagoras informieren möchte, kommt hier zur Übersicht zurück. Dort gibt es auch Übungsaufgaben mit Lösungen zum Thema.