Für den Satz des Pythagoras gibt es die verschiedensten Beweise. Hier in diesem Beitrag wollen wir die besten und verständlichsten zeigen und ihre Funktionsweise erklären. Dabei versuchen wir teilweise mathematische und gezeichnete Beweise einzubeziehen, so dass letztendlich alles verstanden wird.

Satz des Pythagoras Beweis

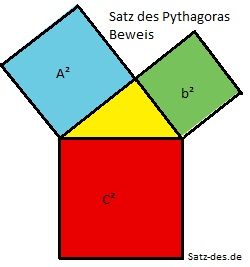
Die Kathetenquadrate

Der Satz des Pythagoras lautet a²+b²=c², was soviel bedeutet, die Quadrate über den Katheten im rechtwinkligen Dreieck sind gleich dem Hypotenusenquadrat.

In unserer Grafik sieht man die Flächen der entstehenden Quadrate, wobei die Summe von A² und b² die gleiche Fläche wie C² haben. In dieser Darstellung ist dies noch schwer zu erkennen, entspricht aber der Wahrheit. Man könnte hier nun die einzelnen Quadrate in Parallelogramme umwandeln und diese dann passend in C² einsetzen. Deutlischer wird der Pythagorasbeweis in unserem nächsten Beispiel, in welchem wir ein Viereck um die Hypotenuse eines rechtwinkligen Dreiecks konstruieren.

Beweis des Satz des Pythagoras geometrisch

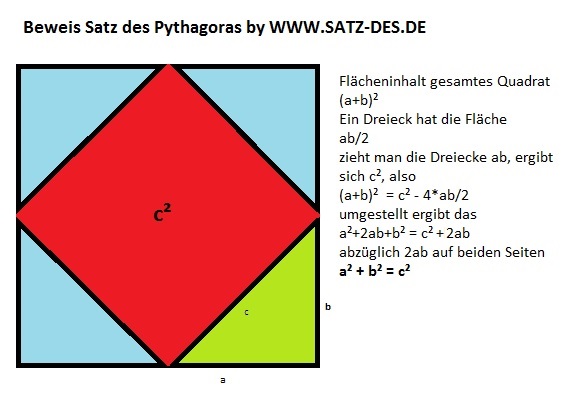
geometrischer Beweis Satz des Pythagoras

Unser rechwinkliges Dreieck sei wie auf der Abbildung mit a,b,c gegeben. Das große Viereck, hat den Flächeninhalt von Kantenlänge (a+b)* Kantenlänge (a+b). Somit ergibt sich kurz geschrieben (a+b)². Zieht man nun von diesem Flächeninhalt die vier einzelnen Dreiecke ab, so bleibt am Ende c² übrig. Alle vier Dreiecke haben dabei einen Flächeninhalt von 2ab, folglich ist (a+b)² = c² + 2ab (das mittlere Viereck c² + die vier Dreiecke).

Löst man nun die Formel auf, ergibt sich dieses:

a²+2ab+b² = c²+2ab

Hier können wir nun ganz einfach -2ab rechnen und erhalten den Satz des Pythagoras

a²+2ab-2ab+b² = c²+2ab-2ab

a²+b² = c²

Somit ist der Satz des Pythagoras bewiesend. Es ist nicht ganz einfach zu verstehen, aber wer mag, darf gerne noch einmal hier unsere Erklärungen zum Satz des Pythagoras lesen.

Zur Übersicht zum Satz des Pythagoras

Zu Satz des Pythagoras Aufgaben mit Lösungen