In diesem Beitrag findet man verschiedene Aufgaben zum Satz des Pythagoras. Die Übungsaufgaben Satz des Pythagoras werden in einem weiteren Beitrag gelöst, den Link dazu findet man jeweils mit einem Klick auf die Überschrift der einzelnen Aufgabe. Wir empfehlen zunächst alle Aufgaben zu rechnen, bevor man sich auf die Lösungen anschaut.

Aufgaben Satz des Pythagoras

Satz des Pythagoras Aufgabe 1

Berechne die jeweils fehlende Seite des Dreiecks ABC, bei dem es sich um ein rechtwinkliges Dreieck handelt.

• a= 8 cm , b= 6 cm, c=?
• a=? , b= 12 cm , c= 13 cm
• a= 7 cm , b= 24 cm, c=?
• a= 3 cm, b= 4 cm, c=?
• a=4 cm, b=?, c= 6 cm

Satz des Pythagoras Aufgabe 2

Schreibe die korrekte Formel für den Satz des Pythagoras auf. Löse die Formel schriftlich auf, so dass die Seite a eines rechtwinkligen Dreiecks berechnet wird.

Textaufgabe Satz des Pythagoras 3

Eine 5 Meter hohe Leiter soll so an eine Wand gelehnt werden, dass sie diese in einer Höhe von 4 Metern berührt. Wie weit steht die Leiter am Boden von der Wand entfernt?

Satz des Pythagoras Textaufgabe 4

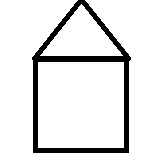Ein Dachdecker soll das Dach des Hausbesitzers nach einem Sturm komplett neu decken. Pro Quadratmeter benötigt er hierzu 20 Dachziegel. Das Haus ist 10 Meter breit und 20 Meter lang.  Das Spitzdach läuft parallel zur langen Seite des Hauses. Die Höhe des Dachs beträgt 4 Meter. Wie viele Dachziegel benötigt der Dachdecker?

Achtung, schwere Aufgabe, für Leute mit Grips!

Übungsaufgabe 5 Satz des Pythagoras

Berechne die fehlende Seite des rechtwinkligen Dreiecks.

• a=7 cm, b=5 cm, c=?
• a=6 cm, b=?, c=9 cm
• a=?, b=12 cm, c=14 cm
• a= 5,5 cm, b=7,6 cm, c=?
• a=2,5 cm, b=?, c=7,9 cm
• a=?, b=3,6 cm, c=11 cm

Satz des Pythagoras Rechenaufgaben 6

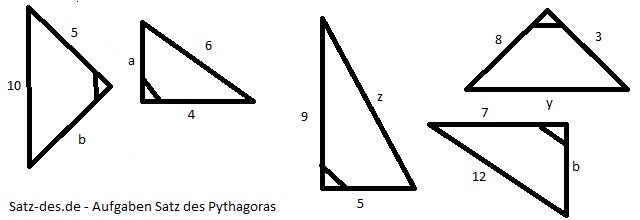
Seitenberechnung nach Pythagoras - Rechenaufgabe

Berechne die fehlenden Seiten auf der Abbildung. Beachte dabei die richtige Bezeichnung.

Weiteres zum Satz des Phytagoras

Dies sind nur die grundlegenden Berechnungen zum Satz des Pythagoras, bei dem jeweils eine Seite berechnet werden muss. Man kann diese Aufgaben jedoch auch mit dem Flächeninhalt eines Dreiecks, sowie in Kombination mit der Dreieckshöhe setzen. Dazu werden in Zukunft weitere Übungsaufgaben hier folgen.

Wer sich noch einmal direkt den Satz des Pythagoras und seine Anleitung anschauen möchte, der sollte hier klicken: Satz des Pythagoras