In diesem Artikel finden sie die Lösung für die 3. Übungsaufgabe Satz des Thales. Schritt für Schritt wird erklärt, wie man zum Ergebnis kommt. Am Ende des Artikels finden sie einen Link, der sie direkt zu den Übungsaufgaben zurück führt. Die Aufgabe lautete: Konstruiere ein rechtwinkliges Dreieck mit AB = 7 cm und Höhe h = 3,5 cm. Zeichne den Thaleskreis dazu ein und erkläre, warum es nur eine Möglichkeit gibt, das Dreieck zu zeichnen.
Lösung Satz des Thales Aufgabe 3
Im ersten Schritt zeichnen wir die Strecke AB mit einer Länge von 7 cm ein. Da wir aus den Angaben wissen, dass zu konstruierende Dreieck hat eine Höhe von 3.5 cm, zeichnen wir parallel zur Strecke AB unsere Höhe h im Abstand von 3.5 cm als eine Gerade ein. Das sieht dann wie auf dieser Abbildung hier aus:
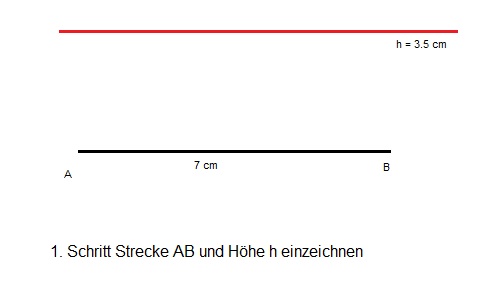
erster Schritt
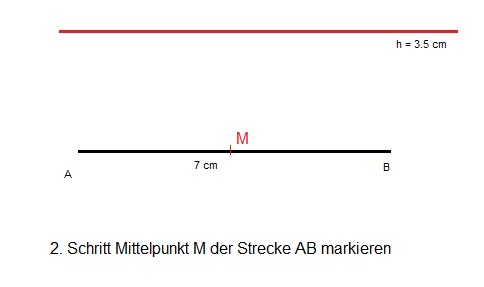
Da wir wissen, dass wir ein rechtwinkliges Dreieck zeichnen müssen, liegt dieses Dreieck zwangsläufig auf einem Thaleskreis. Um den Thaleskreis zu zeichnen suchen wir uns im zweiten Schritt den Mittelpunkt M der Strecke AB.
Nun kann man im dritten Schritt anhand des Mittelpunkts M mit dem Radius AM oder BM den Thaleskreis einzeichnen, der die Rahmenbedingung für alle rechtwinkligen Dreiecke festlegt.
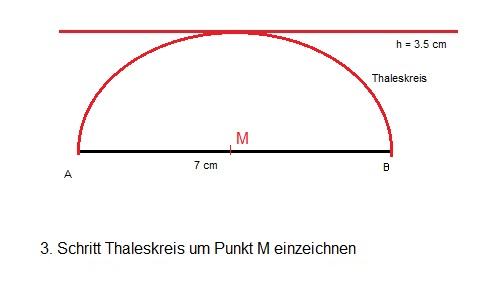
Thaleskreis einzeichnen
Die Höhe h schneidet nun den Thaleskreis und genau an diesem Schnittpunkt zeichnen wir nun in einem letzten Schritt das passende Dreieck ein, indem wir von hier aus die Punkt A und B verbinden.
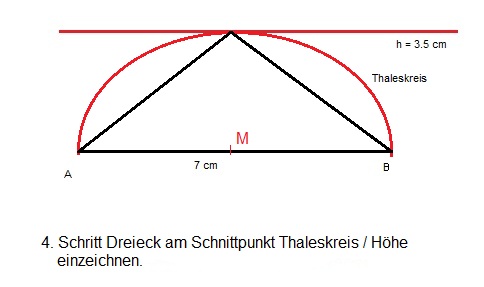
Dreieck am Schnittpunkt einzeichnen
Fertig ist das geforderte Dreieck, aber noch gilt es die Frage zu klären, warum es nur eine Lösungsmöglichkeit gibt.
In dieser Aufgabe beträgt die Höhe h=3.5 cm. Dies entspricht aber auch exakt dem Radius des Thaleskreis und somit die Hälfte der Strecke AB. Dadurch kommt es zur Besonderheit, dass die Höhe h den Thaleskreis nur in einem einzigen Punkt berührt. Die Höhe h ist somit gleichzeitig ein Punkt, in dem der Thaleskreis eine Kreistangente bildet.