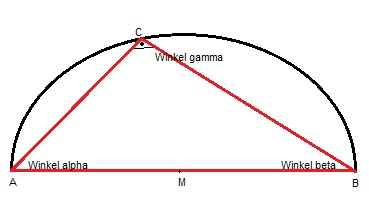
In diesem Beitrag findet man verschiedene Aufgaben zum Satz des Thales. Die Übungsaufgaben Satz des Thales werden in einem weiteren Beitrag gelöst, den Link dazu findet man jeweils mit einem Klick auf die Überschrift der einzelnen Aufgabe. Wir empfehlen zunächst alle Aufgaben zu rechnen, bevor man sich auf die Lösungen anschaut. Alle Rechenaufgaben zum Satz des Thales beziehen sich dabei auf folgende Zeichnung und deren Angaben.

Rechenaufgaben Satz des Thales

Wenn es hier also in einer Aufgabe heißt, A, B oder C sind immer die hier dargestellten Punkte gemeint, ebenso wie die Winkel alpha, beta und gamma und der Mittelpunkt M.

Aufgaben Satz des Thales

Satz des Thales Aufgabe 1:

Welche der folgenden Aussagen sind richtig oder falsch?

1. Jedes rechtwinklige Dreieck liegt auf einem Thaleskreis
2. Die Ecken A, B und C haben alle den gleichen Abstand zum Mittelpunkt M
3. Rechtwinklige Dreiecke sind auch immer gleichschenklig
4. Bei jedem Dreieck, welches auf dem Thaleskreis liegt, gilt gamma = 90°
5. Der Radius eines Thaleskreises ist gleichzeitig auch der Durchmesser
6. Die Höhe eines Dreiecks auf einem Thaleskreis beträgt immer die Strecke M bis C

Satz des Thales Aufgabe 2

Konstruiere mit folgenden Angaben ein Dreieck deiner Wahl auf dem Thaleskreis. Strecke AB = 6 cm. Erkläre in einem Satz, warum es mehrere Möglichkeiten gibt.

Satz des Thales Übungsaufgabe 3

Konstruiere ein rechtwinkliges Dreieck mit AB = 7 cm und Höhe h = 3,5 cm. Zeichne den Thaleskreis dazu ein und erkläre, warum es nur eine Möglichkeit gibt, das Dreieck zu zeichnen.

Textaufgabe Satz des Thales 4

Ulla und Ulf stehen an der Eckfahne am Fußballplatz und wetten, wer schneller an der gegenüberliegenden Eckfahne ankommt. Ulla geht dabei an der Außenlinie entlang (Torseite 68 Meter, Seitenlinie unbekannt)  und Ulf diagonal über den Platz und zwar 125,09 m. Wer von beiden ist schneller? Wie lang ist die Seitenlinie? Kann man hier den Satz des Thales anwenden?

Satz des Thales Aufgabe 5

Gegeben sei ein Dreieck mit alpha = 40°, beta = 50°. Die Strecke AB hat eine Länge von 5 cm. Zeichne das Dreieck. Zeige grafisch, ob das Dreieck auf dem Thaleskreis liegt oder nicht.

Kreistangente Aufgabe 6

Gegeben sei ein Kreis mit deinem Radius r=3 cm. Vom Mittelpunkt des Kreises liegt 7 cm entfernt der Punkt X. Konstruiere eine Kreistangente, die den Punkt X schneidet.

Aufgabe Satz des Thales 7

Beweise mathematisch anhand einer Formel, den Satz des Thales. Erkläre ihn danach in deinen eigenen Worten.

Aufgabe Taleskreis 8

Sind folgende Aussagen wahr oder falsch?

1. Liegt bei einem Dreieck der Punkt C innerhalb des Taleskreises, so ist der Winkel gamma spitz
2. Die Winkel alpha und beta sind bei einem rechtwinkligen Dreieck immer gleich groß
3. Liegt der Punkt C eines Dreiecks auf einem Taleskreis,sind die Winkel alpha und beta automatisch spitz.
4. Liegt Punkt C außerhalb des Taleskreises, so ist Winkel gamma automatisch spitz.
5. Wenn alpha + beta = 90 ° ergeben, liegt das Dreieck automatisch auf dem Taleskreis.